Data Mixing Laws: Optimizing Data Mixture by Predicting Language Modeling Performance

How the mixtures proportions of training data affect the language modeling performance is be quantitatively predictable. This prediction guides tuning data mixture, so as to optimize pretrained model performance, or avoid catastrophic forgetting in continual pretraining.

Introduction

Pretraining data for large language models (LLMs) are typically a mixture of multiple domains (e.g., internet data, academic papers, cods, multimodality data, among other). These data interplay with each other, showing complex interchangeable, unrelated, or contradictory relationships. This necessitates adjusting the mixture proportions of training data to balance the model capabilities while harnessing synergies across domains, thus enhancing the competence of the outcome models. Most existing practices tune the mixture through heuristics to upsample a proportion of high-quality or underrepresented data without disclosing the concrete criteria in detail and it is hard to predate whether these data strategies are effective before finishing the training run.

On the other hand, the advances in scaling lawsdemonstrate that model losses on a given set of evaluation data are quantitatively predictable for a wide range of factors, we wonder whether this also holds for mixture proportions, so that we can estimate the outcome model performance given any mixture before actually training on them, including the desired one that reaches minimum loss. We identify such function and refer to it as data mixing laws.

Furthermore, with the ideas of scaling laws, we can experiment on small scales and apply scaling laws to predict the performance of corresponding data on large-scale training. We can then utilize the predicted losses to establish the data mixing laws to optimize the data mixture for large-scale training. We summarize this pipeline in Fig. 1.

Fig. 1 Illustration on our pipeline to optimize data mixture.

Our work has unveil and validated the data mixing laws as well as the data mixture optimization pipeline. By predicting the overall validation loss, we optimize the training mixture of RedPajama for a 1B model trained on 100B tokens and achieve performance comparable to a model trained on default mixture for 48% more steps. Further applying our data mixing law to continual pretraining can accurately find the proportion that avoids catastrophic forgetting while introducing new capabilities efficiently.

The proportions of data mixtures influence model losses in a quantitatively predictable way

To discover the data mixing laws, we encounter two challenges posed by their characteristics.

• Multi-variables: For the data mixing laws involving K domains, there are K-1 degrees of freedom in the mixture proportions. The increase of variables considerably enlarges the scope of potential functions thereby complicating the identification of the function form.
• Nonmonotonicity: A monotonic relationship between losses and the proportion of any domain indicates that a lopsided mixture can achieve minimum loss without endeavors to balance domain proportions, which contradicts the practice. Therefore, differing from existing scaling laws that loss monotonically decreases with the scale of concerning factors, the data mixing law we study should accommodate non-monotonic functions. This nonmonotonic nature adds another layer of complexity to our analysis.

To navigate these challenges, we initially simplify the problem by studying a scenario where the relationship between loss and mixture proportions fits into a univariate monotonic function then retracts the simplifications progressively. In specific, we begin our study on the case where we only train on two domains thus avoiding multi-variables, and only consider the validation data coming from one of the training domains to circumvent the nonmonotonicity. Subsequently, we broaden our framework to encompass training on multiple domains and explore the predictability of losses on general validation data that also comprises various domains.

Two Training Domains, Single Validation Domain

Fig. 2 demonstrates the predictability of domain losses when training on a two-domain mixtures with different mixture proportions.

Fig. 2 Quantitative predictability of domain losses on two domains (Github and Pile-CC).

We encouragingly find that, for checkpoints with the same size and trained with the same number of steps, after subtracting a shared constant, their domain losses in the log scale demonstrate a linear relationship to the domain proportion. This holds for both domains in our experiments. The result indicates that with other factors fixed, the domain losses of a pretrained language model regarding the domain proportion precisely fit into an exponential law

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ L_{i}(r_i)=c_i+k_i\exp{\left(t_{ii}r_i\right)}

where L_iis validation loss on domain i, r_iis the mixture proportion of domain ic_i,k_i,t_{ii}parameters to fit.

Multiple Training Domains, Single Validation Domain

To accommodate real-world pretraining data that mostly contains more than two domains, we extend our investigation into multiple domains. We base our conjecture of possible forms on the following two principles.

• Compatibility: The form can reduce to that in previous section if the number of training domains is 2
• Symmetry: Any exchanging of variables should not change the functional form.

The second principle stems from the intuition to avoid introducing any domain-specific bias. Together, the two principles lead to candidate functions that replicate the exponential term in two-domain data mixing laws for each training domain and combine them through operations that adhere to commutative law.

Through experiments, we find

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ L_i=c_i+k_i\exp{\left(\sum_{j=1}^{M}t_{ij}r_j\right)}

accurately fits into and predicts the losses under differnt training data mixtures, whereL_iis validation loss on domain ir_jis the mixture proportion of training domain j, c_i,k_i,t_{ii}are parameters to fit. The results are in Fig. 3.

Fig. 3 Prediction results on the domain losses and overall losses in the three-domain experiment.

Multiple Training Domains, Multiple Validation Domains

We further loosen constraints that the validation data are from one of the training domains. We first consider the validation set to be a known composition of the training domains and then free this requirement for more general cases of arbitrary validation sets. These correspond to the two strategies we fit the data mixing laws, which we elaborate on as follows.

Explicit domain aggregation. Considering a validation sets containing K domains with proportionss_{1\dots K}, the validation loss can be written into the weighted sum of domain losses.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~ L=\sum_{i}^{K}s_i L_{i}=\sum_{i}^{K} s_i\left[c_i+k_i\exp{\left(\sum_{j=1}^{M}t_{ij}r_j\right)}\right]

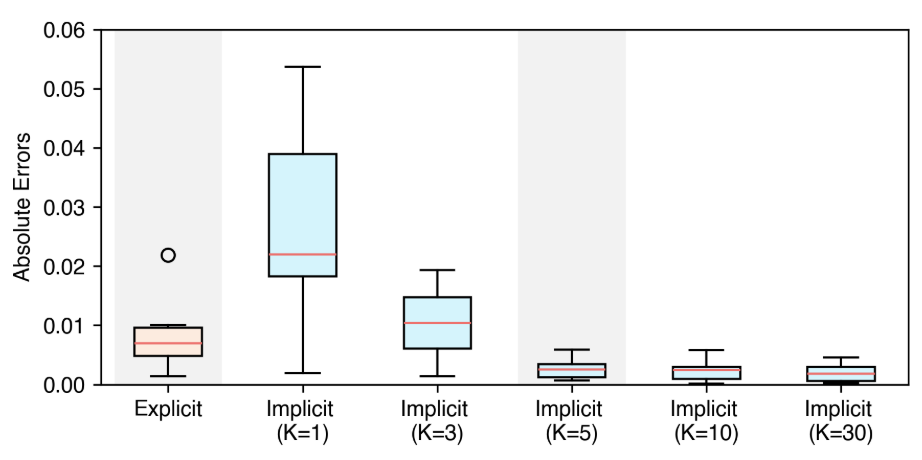
Implicit domain aggregation. A limitation of explicit domain aggregation is that we still need to acquire the components of validation data in advance. This can be inconvenient if the validation set is collected separately from the training ones. For instance, the validation data may come from real-world user queries that cover unknown compositions of various domains. To remove the constraint on validation components, we assume that we can decompose the validation data into K implicit domains whose losses are predictable with the previous data mixing laws for single validation domains. Similar to explicit domain aggregation, we weighted sum the loss of each implicit domains but treating their proportions s_{1\dots K} as learnable parameters as well and fit the overall data mixing laws end to end.

Fig. 4 demonstrate an experiment on five training and validation domains. It shows that implicit domain aggregation fit on par with or better than explicit domain aggregation when the number implicit domain is no fewer than the actual ones.

Fig. 4 The prediction errors on five domain mixtures using explict and implict domain aggregations.

Nested scaling laws predict losses trained on various mixtures using only small-scale experiments

While data mixing laws enable us to predict the performance of models trained on unseen mixtures, the requirement to fit the laws involves training multiple models across diverse mixtures with model sizes and token counts identical to the target ones. Furthermore, we must repeat the experiments for each target model size and training dataset. This results in expensive costs thus hindering the practical value of our data mixing laws

We thus wonder whether we can obtain the losses of different mixture proportions without training at large scales. Fortunately, this idea gains endorsement from existing experiences that verify the impressive extrapolation of scaling laws of training steps and model sizes. We can train small models with few training steps on different mixtures, and fitting scaling laws on them to estimate the losses of the target model size and the target number of training steps. We can then use the predicted losses to fit a data mixing law and search for the optimal mixture. The pipeline is in Fig. 1.

Fig. 5 The validation perplexity on the Pile validation set for 1B models trained on the default mixture and the optimized mixture of RedPajama for 100B tokens.

We apply the proposed pipeline to optimize a 1B model trained for 100B tokens on RedPajama to minimize its validation loss. We adopt the validation set of the Pile to mimic the scenario where validation data are collected separately from the training data. The result suggests that training on the optimzed mixture achieves the performance of models fully trained on the default mixture. And after full training, the optimzed one produces a performance that require 48% more steps if we train on the default mixture as estimated.

Continual Pretraining

We further investigate whether our data mixing laws are also applicable to continual pretraining, which only differs from pretraining by model initialization. Typically, people continually pretrain a pretrained model to inject knowledge from a new domain. To avoid the degradation of the original ability of the pretrained models, namly catastrophic forgetting, a common practice is to continually pretrain on a mixture of orignal pretraining data and the data for the new domain. A too-large proportion for the orignal data herein makes learning new knowledge slow while a too-small one results in catastropic forgetting, thus requiring a careful selection of mixture proportion for a balance.

We find that our data mixing laws are also applicable to continual pretraining, as shown in Fig. 6. With this findings, we can figure out the critical mixture proportion that maintain the model loss in the original pretraining domain which also efficiently enhancing abilties in the new domain.

Fig. 6 Loss prediction and training curves for continually pretraininig Pythia-70M on the mixture of Pile and python codes.

Conclusion

In this work, we explore the quantitative predictability of how data mixtures affect model losses, i.e., the data mixing laws. Our research covers training data from two domains to multiple domains, and validation data from a single domain to combinations of multiple unknown domains. Using data mixing laws, practitioners can estimate the performance of the model on unseen mixture proportions before actual training, thus effectively helps select an ideal data mixture. We further propose nested use scaling laws of training steps, model sizes and our data mixing laww to predict the model performance of different data mixture only through small-scale experiments. The experimental results show that our method effectively optimizes the mixture proportions, resulting in better performance during pre-training, and can guide selecting mixture proportion during continual pre-training to avoid catastrophic forgetting. In summary, we have made a preliminary attempt on the quantitative method of curating data. With the increasing interest in data engineering, we hope that our exploration will facilitate further quantitative research and theoretical analysis in this area.